Black-Scholesov vzorec
:: Repetitio est mater studiorum ::
Tak ako minulý týždeň, začneme opakovaním. Na začiatku cvičenia teda vypočítame nejaké príklady podobné tým, ktoré sme robili na predchádzajúcih cvičeniach:
- Nájdite riešenie stochastickej diferenciálnej rovnice
 .
.
Návod: Napíšte stochastickú diferenciálnu rovnicu, ktorú spĺňa proces 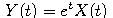 .
.
- V súbore orcl.txt sú denné dáta cien akcií (najstaršie sú na začiatku). Predpoklajme, že cena akcie sa riadi procesom
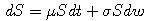 .
.
- Odhadnite z dát parametre tohto procesu.
- Vypočítajte pravdepodobnosť, že o pol roka bude cena akcie aspoň o 30 percent vyššia ako dnes.
- Nájdite pravdepodobnostné rozdelenie ročných výnosov.
- Nájdite stratégiu s nasledovným payoffom:
:: Black-Scholesova parciálna diferenciálna rovnica ::
Pripomeňme si, že cena V(S,t) ľubovoľného derivátu európskeho typu spĺňa Black-Scholesovu parciálnu diferenciálnu rovnicu
kde
- S je cena akcie,
- t je čas
- T je čas expirácie derivátu
- r je bezriziková úroková miera
 je volatilita ceny akcie, o ktorej predpokladáme, že sa riadi geometrickým Brownovym pohybom
je volatilita ceny akcie, o ktorej predpokladáme, že sa riadi geometrickým Brownovym pohybom
Podľa druhu derivátu sa k rovnici pridáva koncová podmienka
V(S,T) v čase expirácie.
:: Cvičenia (1) ::
- Dosadením overte, že nasledujúce funkcie sú riešením Black-Scholesovej parciálnej diferenciálnej rovnice:
- V(S,t) = c S, kde c je kladná konštanta
- V(S,t) = c e-r(T-t) kde c je kladná konštanta
Aké deriváty predstavujú tieto riešenia?
- Dokážte:
- Ak payoff V(S,T) je nezáporný, tak aj V(S,t) je nezáporná funkcia pre každé S > 0, 0 < t < T.
- Ak payoff V(S,T) je nezáporný a ostro kladný pre S z nejakého intervalu, tak V(S,t) je ostro kladná funkcia pre každé S > 0, 0 < t < T.
Aká je finančná interpretácia týchto tvrdení?
- Dokážte, že ak V je riešením Black-Scholesovej PDR, tak aj
 je riešením. Použite túto vlastnosť riešenia na dôkaz nasledovného tvrdenia: Ak je derivácia payoffu
je riešením. Použite túto vlastnosť riešenia na dôkaz nasledovného tvrdenia: Ak je derivácia payoffu 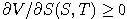 nezáporná pre každé S > 0, tak aj derivácia
nezáporná pre každé S > 0, tak aj derivácia
 je nezáporná pre každé S > 0, t < T. Aká je jeho interpretácia?
je nezáporná pre každé S > 0, t < T. Aká je jeho interpretácia?
:: Ďalšie príklady na precvičenie ::
-
Nájdite všetky riešenia Black-Scholesovej rovnice, ktoré majú tvar V=V(S). Týmto spôsobom nájdete všetky také deriváty, ktoré môže na trhu
existovať (a nevytvoria arbitráž), ktorých hodnota závisí len aktuálnej ceny akcie, ale nie od času.
- Dokážte, ak je druhá derivácia payoffu
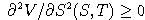 nezáporná pre každé S > 0, tak aj druhá derivácia ceny
nezáporná pre každé S > 0, tak aj druhá derivácia ceny
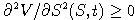 je nezáporná pre každé S > 0, 0 < t < T.
je nezáporná pre každé S > 0, 0 < t < T.
 .
. 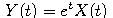 .
.
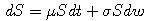 .
.


 je volatilita ceny akcie, o ktorej predpokladáme, že sa riadi geometrickým Brownovym pohybom
je volatilita ceny akcie, o ktorej predpokladáme, že sa riadi geometrickým Brownovym pohybom
 je riešením. Použite túto vlastnosť riešenia na dôkaz nasledovného tvrdenia: Ak je derivácia payoffu
je riešením. Použite túto vlastnosť riešenia na dôkaz nasledovného tvrdenia: Ak je derivácia payoffu 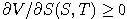 nezáporná pre každé S > 0, tak aj derivácia
nezáporná pre každé S > 0, tak aj derivácia
 je nezáporná pre každé S > 0, t < T. Aká je jeho interpretácia?
je nezáporná pre každé S > 0, t < T. Aká je jeho interpretácia?
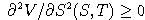 nezáporná pre každé S > 0, tak aj druhá derivácia ceny
nezáporná pre každé S > 0, tak aj druhá derivácia ceny
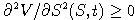 je nezáporná pre každé S > 0, 0 < t < T.
je nezáporná pre každé S > 0, 0 < t < T.